Building a Competitive AI for Flood-It
Contents
Table of Contents
▼
Being an absolute undefeated master of Filler, I recently built a complete end-to-end system that trains a Deep Q-Network (DQN) to play Flood-It/Filler, a territory-capture puzzle game, and deployed it as an interactive web application with real-time AI decision visualization.[*](Algorithm reference: "Playing Atari with Deep Reinforcement Learning" by Mnih et al. (2013), which introduced DQN for discrete action spaces.) The project demonstrates how modern reinforcement learning can be applied to strategic games, with full transparency into the AI's decision-making process.

46 wins in Filler built brick by brick.
Flood-It presents an interesting challenge for RL: it combines discrete action selection with strategic territory planning. Unlike pure reflex games (like Atari), success requires understanding spatial relationships and opponent behavior. Unlike pure strategy games (like Chess), the state space is manageable enough for deep learning to excel.
The Game: Flood-It as an RL Problem
Flood-It is played on an grid where each cell contains one of colors. Two players start from opposite corners—Player 1 from (top-left) and Player 2 from (bottom-right). On each turn, a player selects a color , and all cells connected to their current territory that match color become theirs.
The game terminates when all cells are claimed: , where is the territory of player . The winner is the player with more cells: .
For this implementation, I used , , and , creating a state space of possible board configurations. While this is intractable for tabular methods, it's well-suited for function approximation via deep neural networks.
Architecture: A Modular RL System
The system is architected in three layers, each with clear responsibilities:
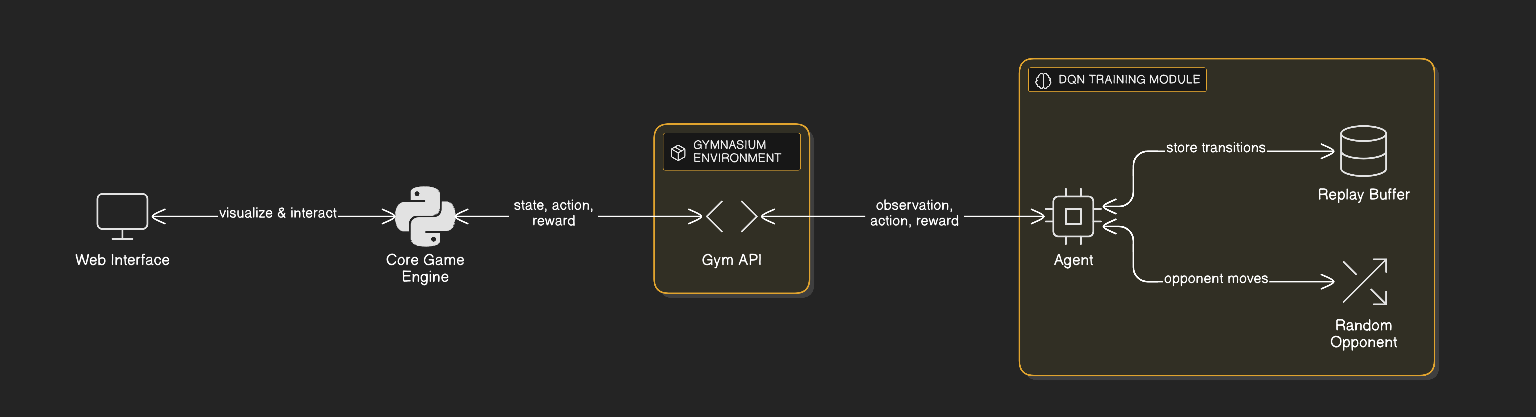
System Architecture: The three-layer design separates game logic, RL training, and web interface for modularity and maintainability.
1. Core Game Engine
The foundation is a pure Python game engine (core_game.py) that implements the flood-fill algorithm. Given a starting position and a target color , the algorithm computes the connected component:
This is implemented via a breadth-first search, ensuring complexity per move. The engine also enforces game rules: players cannot select their current color or the opponent's last move, preventing trivial strategies.
2. Gymnasium Environment Wrapper
To integrate with RL frameworks, I wrapped the game in a Gymnasium environment (gym_env.py).[*](Framework reference: Gymnasium, the maintained fork of OpenAI Gym.)
Observation Space: The state is encoded as a one-hot tensor where:
This encoding is crucial—it tells the neural network that colors are categorical, not numerical values. The difference between "red" and "blue" is fundamental, not just "1" and "2".
Action Space: Discrete actions , where represents selecting color .
Reward Function: The reward signal combines immediate gains with terminal bonuses:
where is the change in territory size. The heavy penalty for invalid moves () encourages the policy to learn valid action selection, while the terminal bonuses () provide clear signal for winning vs. losing.
Training Opponent: During training, the AI (Player 1) faces a random opponent (Player 2). This stochasticity prevents overfitting to deterministic strategies and encourages robust play.
Training Visualization: The AI learns to capture territory strategically against a random opponent during training.
3. Deep Q-Network Training
I implemented the training pipeline using Stable Baselines3's DQN.[*](Framework reference: Stable Baselines3 by Raffin et al. (2021), providing reliable implementations of RL algorithms.)
DQN learns an action-value function that estimates the expected return:
where is the discount factor. The optimal policy selects actions greedily:
The network architecture uses a Multi-Layer Perceptron (MLP) policy since the observation is already a structured tensor. The input shape is after flattening, with hidden layers of sizes and ReLU activations.
Training Configuration:
- Algorithm: DQN with experience replay and target network
- Learning Rate:
- Discount Factor:
- Timesteps:
- Batch Size:
- Replay Buffer: transitions
The training loop follows the standard DQN algorithm:[*](Algorithm details from Mnih et al. (2013) and "Human-level control through deep reinforcement learning" by Mnih et al. (2015).)
- Collect transition in replay buffer
- Sample minibatch from buffer
- Compute target:
- Update: where
The target network is updated periodically to stabilize learning.
The Challenge: Player Perspective Mismatch
A critical architectural challenge emerged: the model trains as Player 1 (starting from top-left) but must play as Player 2 (starting from bottom-right) in the deployed game. I solved this by flipping the board horizontally and vertically before feeding it to the model, then using the action directly.
where and are horizontal and vertical flips, respectively. This transforms the bottom-right corner to top-left, allowing the model to see the board from its training perspective.
The transformation is applied before inference:
def flip_board_for_p2(board):
"""Transform board so P2 perspective becomes P1 perspective"""
return np.flip(np.flip(board, axis=0), axis=1)
This elegant solution avoids retraining and maintains the model's learned strategies.
Real-Time Inference: Q-Value Extraction
To provide transparency into the AI's decision-making, I extract Q-values for all actions. Stable Baselines3 doesn't expose this directly, so I access the underlying Q-network:
obs_tensor = model.policy.obs_to_tensor(obs)[0]
model.policy.q_net.eval()
with torch.no_grad():
q_values = model.policy.q_net(obs_tensor).cpu().numpy()[0]
This gives us the vector , which we visualize in the frontend.
Invalid Action Filtering: The raw Q-values may suggest invalid actions (current color or opponent's last move). I filter the action space:
Then select:
This ensures the AI never makes illegal moves while still leveraging its learned value estimates.

Q-Value Transparency: The frontend displays Q-values for all actions, showing the AI's evaluation of each color choice. The chosen action (highlighted in green) typically has the highest Q-value among valid options.
Web Interface: Real-Time Decision Visualization
The frontend (React) provides an immersive experience with several key features:
Territory Visualization: Each cell displays its owner via colored borders:
- Blue border: Player 1 territory
- Red border: Player 2 (AI) territory
The visualization uses CSS ::after pseudo-elements with subtle animations to indicate ownership without cluttering the board.
Q-Value Display: For each AI move, the interface shows:
- A bar chart of Q-values for all 6 colors
- The chosen action highlighted
- Invalid actions grayed out
- Numerical Q-values for transparency
This transparency is crucial for understanding and trusting the AI's decisions. Users can see, for example, that the AI might prefer color 3 (Q-value: 12.4) over color 1 (Q-value: 8.2), providing insight into its strategic reasoning.
Move History: A collapsible log maintains a complete record of all AI decisions, allowing users to analyze patterns in the AI's play over the course of a game.
Gameplay Demo: Real-time gameplay showing territory expansion, Q-value visualization, and AI decision-making in action.
Training Results and Analysis
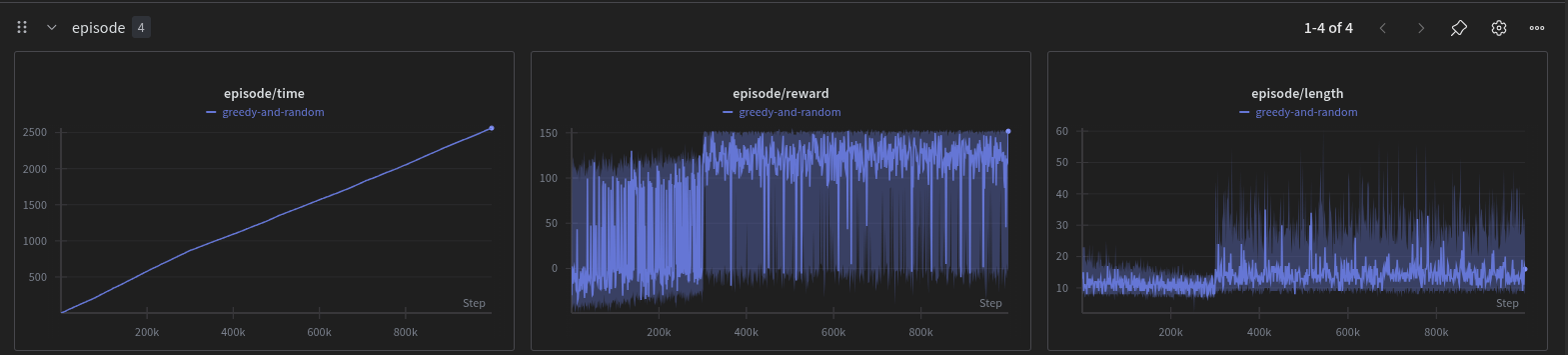
After training for 500,000 timesteps, the AI demonstrates several learned behaviors:
Strategic Play: The policy learns to prioritize moves that maximize immediate territory gain. The Q-function develops clear preferences, with some colors consistently valued higher than others based on board state.
Invalid Move Avoidance: The heavy penalty () for invalid moves causes the policy to learn valid action selection early in training. The network learns to recognize its current color and avoid selecting it.
Adaptability: The model generalizes to different board configurations. Since training uses random board generation, the policy must learn robust strategies that work across varied initial states.
Q-Value Patterns: Analysis of extracted Q-values reveals:
- Clear separation between high-value and low-value actions
- Consistent preferences for certain colors in similar board states
- Adaptation to opponent behavior (though opponent is random during training)
The learning curve shows steady improvement in mean episode reward, with the policy transitioning from random play to strategic territory capture.
Technical Implementation Details
Backend Architecture
The API (api.py) uses FastAPI with WebSocket support for real-time communication:[*](Framework reference: FastAPI, a modern Python web framework.)
- Model Loading: The trained DQN is loaded once at startup, avoiding repeated disk I/O
- State Management: Each WebSocket connection maintains its own game instance
- Message Protocol: JSON messages with types
INIT,MOVE,UPDATE, andGAME_OVER
The WebSocket protocol enables low-latency updates, with the entire game loop (player move → AI inference → state update) completing in milliseconds.
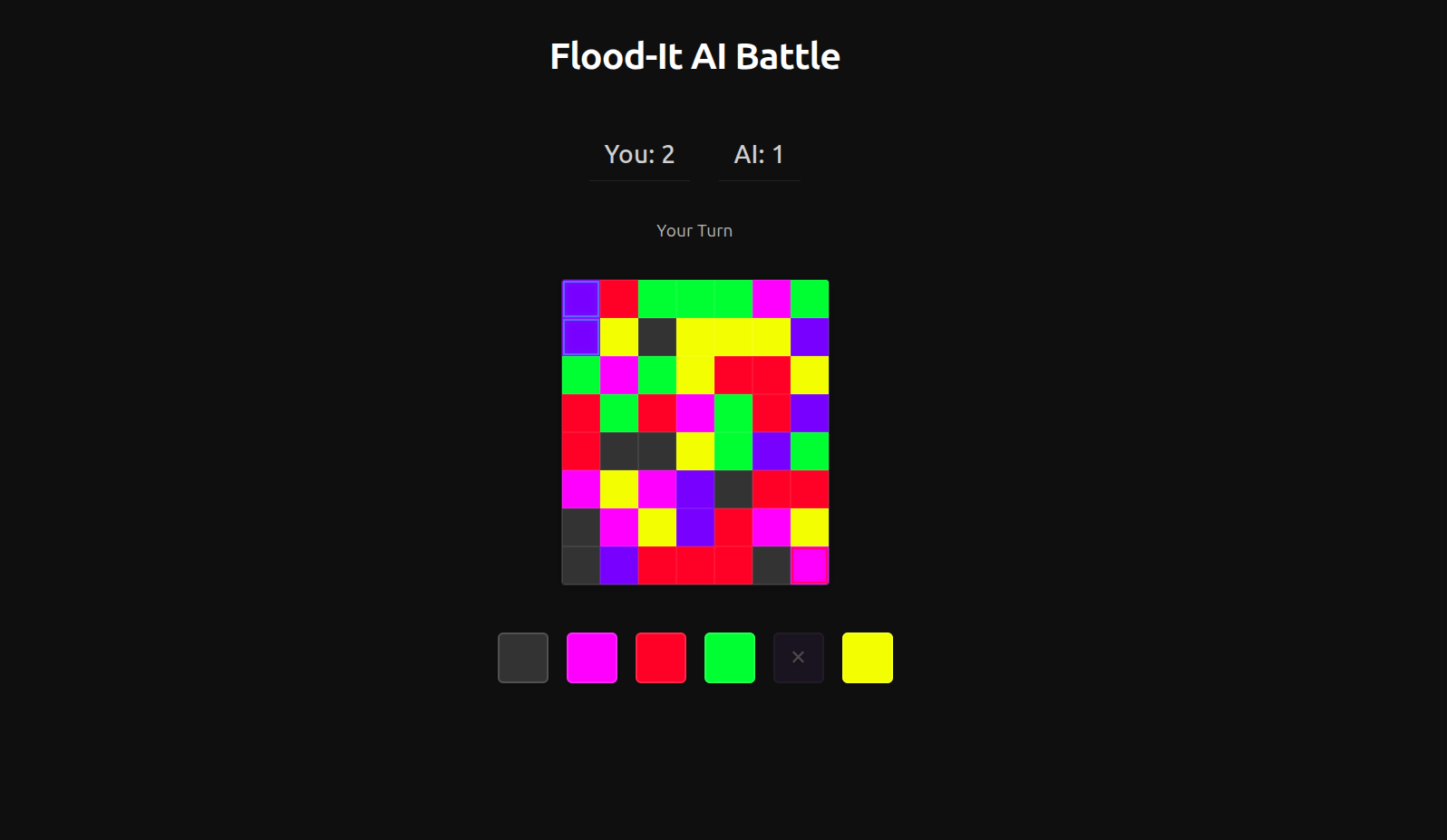
User Interface: The polished dark-mode interface with territory visualization, Q-value displays, and collapsible AI move history.
Frontend Design
The React frontend follows a minimalistic dark-mode design philosophy:
- Responsive Layout: Uses CSS
clamp()for fluid typography and spacing - Smooth Interactions: All transitions use cubic-bezier easing functions
- Custom Scrollbars: Styled scrollbars for the AI log panel
- Territory Animations: Subtle pulse animations for territory indicators
The design prioritizes clarity and user experience, with every visual element serving a purpose.
Mathematical Formulation of the Reward
The reward function can be expressed more formally. Let and be the territories at time , and let be the change in territory size.
The reward for a valid move is:
where and are terminal bonuses, and is the indicator function.
For invalid moves:
where is the penalty magnitude.
The total return for an episode is:
where is the episode length. The discount factor ensures the agent values both immediate gains and long-term strategic positioning.
Comparison with Alternative Approaches
Tabular Q-Learning: The state space is intractable for tabular methods. Even with state abstraction, the number of states exceeds , making function approximation necessary.
Policy Gradient Methods: While PPO could work,[*](Algorithm reference: "Proximal Policy Optimization Algorithms" by Schulman et al. (2017).) DQN's value-based approach provides interpretable Q-values, which are crucial for the transparency features in the web interface.
Monte Carlo Tree Search (MCTS): MCTS could provide strong play,[*](Algorithm reference: "Mastering the game of Go without human knowledge" by Silver et al. (2017).) but requires significant computational resources per move. DQN's feedforward inference is orders of magnitude faster, enabling real-time gameplay.
Future Enhancements
Several directions could improve the system:
Self-Play Training: Training the AI against itself (rather than a random opponent) could lead to stronger play through iterative improvement, similar to AlphaZero.[*](Algorithm reference: "Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm" by Silver et al. (2017).)
Longer Training: Increasing timesteps to or more could improve performance, though diminishing returns are expected.
Architecture Improvements: Using a CNN policy (treating the board as an image) might capture spatial patterns better, though the current MLP performs adequately.
AI vs Human Gameplay: A complete game showing the trained AI competing against a human player, demonstrating learned strategic behavior.
Multi-Agent RL: Training multiple agents with different strategies could create a more diverse and challenging opponent pool.
Conclusion
Beyond the architecture and the math, this project was simply a blast to build. There is something uniquely satisfying about watching an agent—which started out making completely random moves—slowly derive a winning strategy that eventually rivals your own. It bridges the gap between abstract RL theory and a tangible, playable experience.
The combination of deep reinforcement learning, real-time visualization, and thoughtful design creates an application that is both technically impressive and genuinely engaging. The AI's learned strategies, visible through Q-value analysis, reveal the power of modern RL for strategic game playing. Hopefully we see more of this in the wild to help inspire and educate more experiments.
Technical Stack: Python 3.13+, Stable Baselines3, Gymnasium, FastAPI, React, PyTorch
Code Repository: Available with complete documentation and setup instructions