Support Vector Machines
Contents
Table of Contents
▼
Support Vector Machines (SVMs) are versatile machine learning models capable of handling various tasks, including classification, regression, and novelty detection.[*](Primary reference: Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow by Aurélien Géron (3rd edition, 2022).) What makes SVMs particularly powerful is their ability to find optimal decision boundaries by maximizing the margin between classes, making them robust and effective for both linear and nonlinear problems. This margin-maximization principle, combined with the elegant kernel trick for handling nonlinear data, has made SVMs one of the most influential algorithms in machine learning.
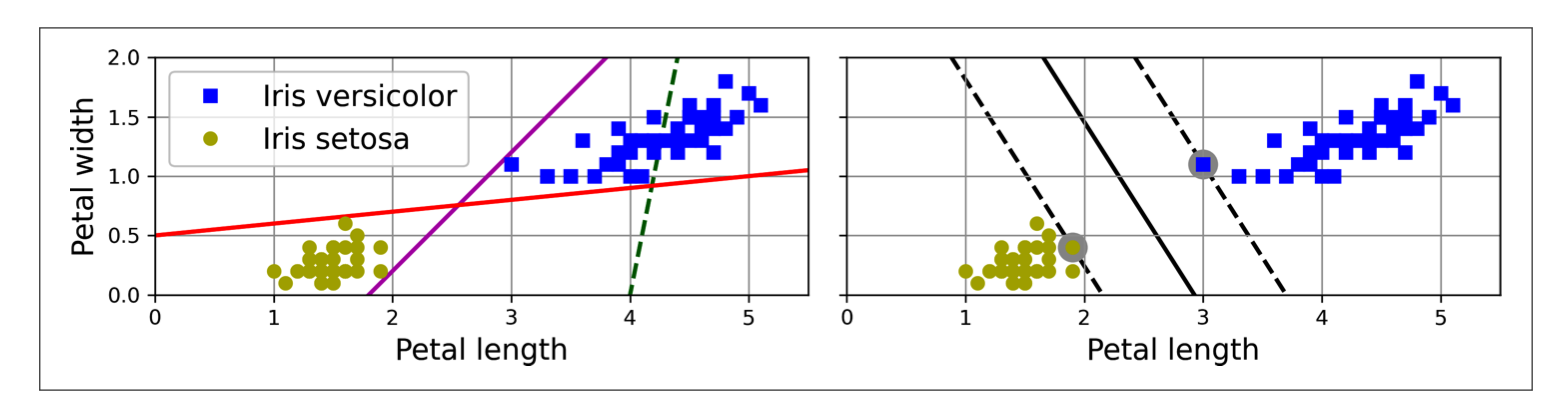
Maximum Margin Classification: An SVM finds the optimal decision boundary that maximizes the margin between classes, with support vectors defining the margin.
Mathematical Foundations
Decision Function
At their core, SVMs make predictions using a decision function. For a linear SVM, the decision function takes the form:
where:
- is the weight vector
- is the input feature vector
- is the bias term
If the decision function output is positive, the instance is classified as belonging to the positive class; otherwise, it belongs to the negative class. The magnitude of the output also indicates the confidence of the prediction—instances farther from the decision boundary are classified with higher confidence.
Training and Optimization
Training an SVM involves finding the optimal values for the weight vector and the bias term . The objective is to maximize the margin between the classes while minimizing margin violations. This can be formulated as a constrained optimization problem that seeks the hyperplane with the largest possible margin.
Hard Margin vs. Soft Margin Classification
Hard Margin Classification assumes data is perfectly linearly separable, which is rarely the case in real-world scenarios. It is sensitive to outliers and can fail when the data contains noise or mislabeled instances.

Hard Margin Classification: Assumes perfect linear separability, making it sensitive to outliers and noise in the data.
Soft Margin Classification allows for some misclassifications (margin violations) by introducing slack variables that are penalized in the optimization objective. The regularization parameter controls the trade-off between a large margin and minimizing margin violations.
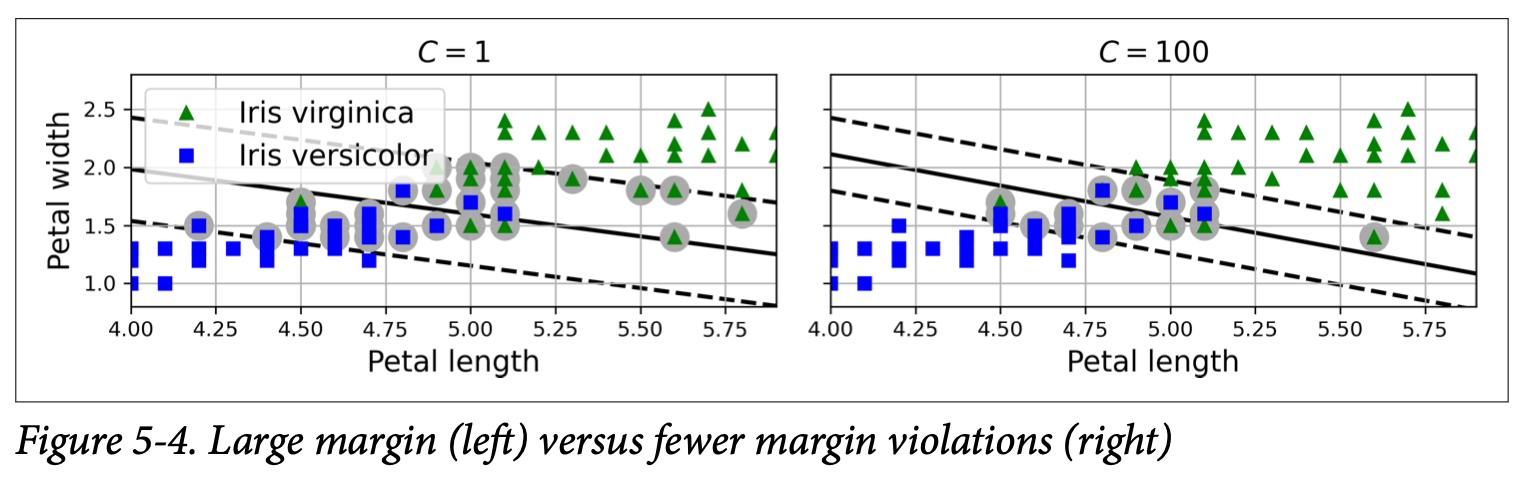
Soft Margin Classification: Allows margin violations controlled by the regularization parameter C. Lower C values create wider margins but more violations, while higher C values create narrower margins with fewer violations.
The regularization hyperparameter plays a crucial role in controlling the model's behavior. When creating an SVM model using Scikit-Learn, setting to a low value results in a wider margin but more margin violations, effectively regularizing the model and reducing the risk of overfitting. With a high value, the margin becomes narrower, and the model becomes more sensitive to individual data points, potentially leading to overfitting. The key is finding the right balance: reducing makes the margin larger and the model more robust, but reducing it too much can lead to underfitting.
Comparing SVM Algorithms in Scikit-Learn
Scikit-Learn provides several SVM implementations, each optimized for different use cases:
| Algorithm | Advantages | Disadvantages | Kernel Functions | Suitable for... |
|---|---|---|---|---|
| LinearSVC | Fast and efficient, especially for large datasets | Does not support kernel functions | No | Linearly separable data |
| SVC | Handles both linear and nonlinear classification | Slower than LinearSVC, particularly for large datasets | Yes | Small to medium-sized datasets, especially for nonlinear classification |
| SGDClassifier | Suitable for online learning and very large datasets due to stochastic gradient descent | Does not support kernel functions | No | Large datasets that may not fit in memory (out-of-core learning) |
Nonlinear SVM Classification
While linear SVMs excel at classifying linearly separable data, real-world datasets often exhibit intricate, nonlinear relationships that defy separation by a simple straight line. Nonlinear SVMs rise to this challenge by employing ingenious techniques that empower them to craft more sophisticated, nonlinear decision boundaries.
Augmenting Feature Space with Polynomial Features
This method enhances the original feature set by introducing polynomial features. For instance, if the original features are and , we might add , , and as new features. This transformation allows linear SVM algorithms to discern nonlinear relationships between features.
Illustrative Example: Incorporating a squared feature () can transform a non-linearly separable 1D dataset into a linearly separable 2D dataset.
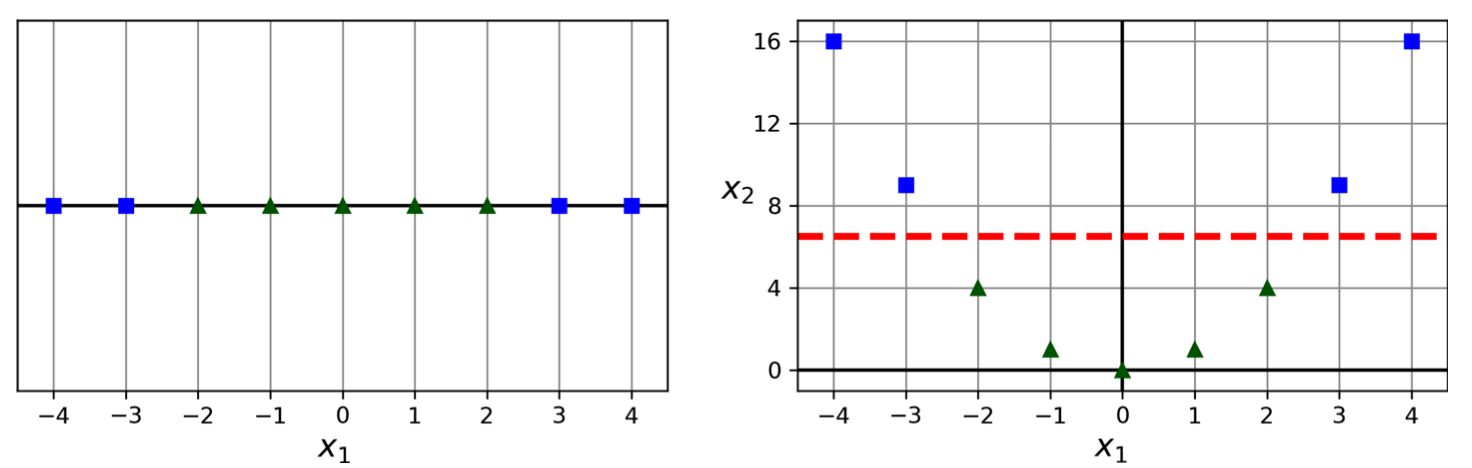
Polynomial Feature Transformation: Adding polynomial features transforms nonlinear data into a higher-dimensional space where it becomes linearly separable.
Implementation: The PolynomialFeatures transformer in Scikit-Learn can be integrated into a machine learning pipeline to achieve this.[*](Scikit-Learn documentation: PolynomialFeatures.)
Drawbacks: This approach can lead to a combinatorial explosion of features as the polynomial degree increases, potentially hindering computational efficiency. For a dataset with features and polynomial degree , the number of features grows as , which can become prohibitively large.
The Kernel Trick: Navigating High Dimensions
The kernel trick provides an elegant solution to the computational hurdle posed by high-degree polynomial features.[*](For more on kernel methods, see Wikipedia: Kernel Method.) It grants SVMs the ability to operate in a high-dimensional feature space implicitly, without explicitly calculating all the transformed features.
Mathematical Intuition: The kernel trick capitalizes on the fact that numerous SVM algorithms depend solely on the dot product between data points. Certain kernel functions, like the polynomial kernel, can compute the dot product of transformed vectors in a high-dimensional space using only the original vectors.
Illustrative Example: Consider a second-degree polynomial kernel: . This kernel computes the dot product of vectors transformed by a second-degree polynomial mapping function without explicitly performing the transformation. Notice that this mapping function transforms the original 2D vectors into 3D vectors.
The dot product of these transformed vectors, , can be calculated directly using the original vectors as follows:
This demonstrates that the kernel function effectively computes the dot product in the higher-dimensional space without requiring the explicit calculation of the transformed vectors.
Popular Kernels
Polynomial Kernel:
where:
- is the degree of the polynomial
- (gamma) controls the influence of each training example
- (coef0) is an independent term
Gaussian Radial Basis Function (RBF) Kernel:
where:
- controls the influence of each training example (larger means closer examples have more influence)
- The RBF kernel maps data to an infinite-dimensional space
Mercer's Theorem: This theorem establishes the theoretical basis for the kernel trick, guaranteeing the existence of a valid mapping function for kernel functions that meet specific mathematical criteria.[*](For more on Mercer's theorem, see Wikipedia: Mercer's Theorem.) This assures us that the kernel function computes a dot product in a legitimate higher-dimensional space.
Implementation: The SVC class in Scikit-Learn facilitates the use of various kernels.[*](Scikit-Learn documentation: Support Vector Machines.) Set kernel="poly" for the polynomial kernel or kernel="rbf" for the Gaussian RBF kernel.
Hyperparameters: Kernels typically have hyperparameters that require tuning for optimal performance. For example, the polynomial kernel utilizes the degree (degree) and coefficient (coef0) hyperparameters, while the RBF kernel has the gamma (gamma) hyperparameter. These hyperparameters significantly impact model performance and should be carefully tuned using techniques like grid search or randomized search.
Kernel Selection Guide for SVMs
Choosing the right kernel is crucial for SVM performance. Here's a guide to help you select the appropriate kernel for your problem:
| Kernel | Advantages | Considerations |
|---|---|---|
| Linear | Computational efficiency: LinearSVC scales efficiently for large datasets | Suitable for linearly separable data; may underperform on nonlinear datasets |
| Gaussian RBF | Excellent for nonlinear data; often performs well in nonlinear scenarios | Computational cost can be slow for very large datasets; requires careful tuning of gamma parameter |
| Polynomial | Good for capturing polynomial relationships in data | Hyperparameter tuning required (degree, gamma, coef0); can be computationally expensive for high degrees |
| Other Kernels | Specialized kernels: Consider kernels designed for specific data structures (e.g., string kernels for text) | Hyperparameter tuning may require experimentation to find optimal hyperparameters |
SVM Regression
Instead of striving to find the widest "street" separating different classes, SVM Regression aims to fit a hyperplane that encompasses as many data points as possible within a defined margin of error.
This margin of error is determined by the hyperparameter epsilon (). The figure below illustrates how different epsilon values influence the width of the margin and the number of support vectors.
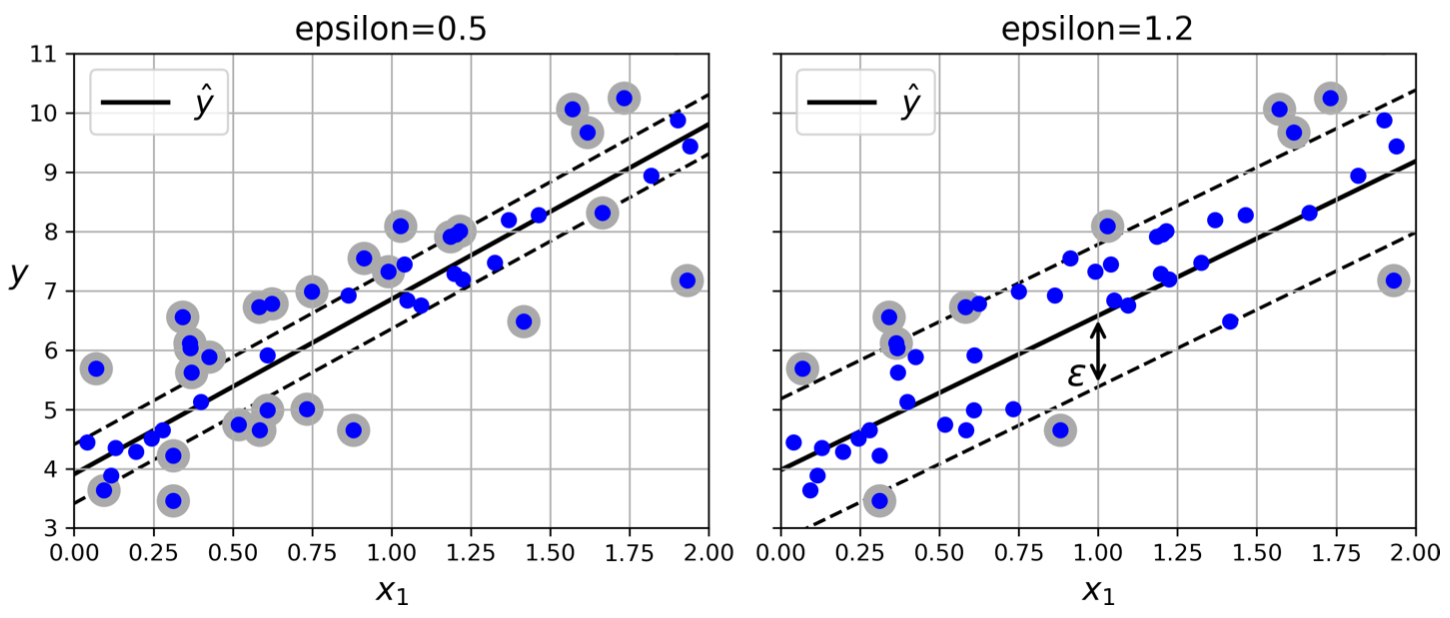
SVM Regression: Different epsilon () values control the width of the margin and the number of support vectors in SVM regression.
Key Concepts in SVM Regression
-
Goal: The primary goal is to fit as many data points as possible within the margin defined by epsilon () while minimizing the instances that fall outside this margin.
-
Epsilon-Insensitivity: A crucial characteristic of SVM Regression is epsilon-insensitivity.[*](Original SVM regression paper: Support Vector Regression by Drucker et al. (1996).) This implies that predictions remain unaffected by data points situated within the margin. This property contributes to the robustness of SVM Regression, as it is less susceptible to minor fluctuations in the data.
-
Regularization with Epsilon: The epsilon value acts as a regularization parameter. Decreasing epsilon leads to a narrower margin, increasing the number of support vectors and regularizing the model. This helps prevent overfitting. Conversely, increasing epsilon creates a wider margin with fewer support vectors, potentially leading to underfitting if set too high.
The optimization problem for SVM regression seeks to minimize:
subject to constraints that ensure most points fall within the -tube, where and are slack variables for points above and below the margin, respectively.
Conclusion
Support Vector Machines represent a powerful and theoretically grounded approach to machine learning that has stood the test of time. Their ability to find optimal decision boundaries through margin maximization, combined with the elegant kernel trick for handling nonlinear data, makes them versatile tools for both classification and regression tasks.
The key to successfully applying SVMs lies in understanding the trade-offs:
-
Linear vs. Nonlinear: Choose
LinearSVCfor large, linearly separable datasets, andSVCwith appropriate kernels for nonlinear problems. -
Regularization: The parameter controls the balance between margin width and classification accuracy. Lower values provide more regularization, while higher values can lead to overfitting.
-
Kernel Selection: The Gaussian RBF kernel is often a good default for nonlinear problems, but polynomial kernels can be effective when polynomial relationships are expected. Always tune kernel hyperparameters carefully.
-
Scalability: For very large datasets, consider
LinearSVCorSGDClassifierwith linear kernels, as they scale better than kernelized SVMs.
While modern deep learning has overshadowed SVMs in some domains, they remain valuable tools, especially when interpretability, robustness, and theoretical guarantees are important. The margin-maximization principle and kernel trick continue to influence modern machine learning, appearing in various forms in neural networks and other advanced algorithms.